Evaluación 4: Programación 1
Números polares Y Rectangulares
Números Polares:
La forma polar de un número complejo es otra forma de representar un número complejo. La forma z = a + bi es llamada la forma coordenada rectangular de un número complejo.
El eje horizontal es el eje real y el eje vertical es el eje imaginario. Encontramos los componentes reales y complejos en términos de r y θdonde r es la longitud del vector y θ es el ángulo hecho con el eje real.
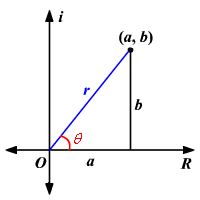
Números rectangulares:
Los números que no son primos se pueden descomponer en varias partes iguales, lo que quiere decir que se pueden poner como un rectángulo, por lo que les llamaremos números rectangulares; por ejemplo el 12 que se puede dividir en dos tantos de seis (o en seis de dos), para formar un rectángulo de 2 por 6, es un número rectangulares.
Aplicación a la programación
ALGORITMO
#include <iostream>
#include <math.h>
using namespace std;
int main()
{
double r1,r2,y1,x1,x2,y2,x,y,r,ttha,r3,r4,phi1,phi2,RAD1,RAD2,pi=1.141592;
cout<<"***************************** \n";
cout<<"Numeros Complejos \n";
cout<<"Ingrese R1: ";cin>>r1;
cout<<"Ingrese R2: ";cin>>r2;
cout<<"Ingrese el angulo: ";cin>>ttha;
//conversion de angulo
RAD1=(2*pi*ttha)/360;
RAD2=(2*pi*ttha)/360;
//conversion a rectangulares
x1=r1*cos(RAD1);
y1=r1*sin(RAD1);
x2=r2*cos(RAD2);
y2=r2*sin(RAD2);
cout<<"1)Conversion R -> P \n";
cout<<"z1= "<<(x1+x2)<<" +j "<<(y1+y2)<<endl;
//conversion a polares
r=sqrt(pow((x1+x2),2)+pow((y1+y2),2));
phi1= atan((y1+y2)/(x1+x2));
cout<<"radio "<<r<< " angulo "<<ttha<<endl;
cout<<" \n"<<endl;
cout<<" \n"<<endl;
cout<<"2)Conversion P -> R \n";
r=sqrt(pow((x1+x2),2)+pow((y1+y2),2));
phi1= atan((y1+y2)/(x1+x2));
cout<<"radio "<<r<< " angulo "<<ttha<<endl;
cout<<"z1= "<<(x1+x2)<<" +j "<<(y1+y2)<<endl;
cout<<" \n"<<endl;
cout<<" \n"<<endl;
cout<<"3)Suma -> R \n";
cout<<"z1= "<<(x1+x2)<<" +j "<<(y1+y2)<<endl<<endl;
cout<<" \n"<<endl;
cout<<" \n"<<endl;
cout<<"4)Divide -> p \n";
r3=sqrt(x1*x1+y1*y1);
r4=sqrt(pow(x2,2)+pow(y2,2));
phi1=atan(y1/x1);
phi2=atan(y2/x2);
cout<<"radio= "<<(r3/r4)<<" angulo= "<<(phi1-phi2)<<endl;
cout<<" \n"<<endl;
cout<<" \n"<<endl;
cout<<"5)Suma -> p \n";
cout<<"radio= "<<(r3+r4)<<" angulo= "<<(phi1+phi2)<<endl;
cout<<" \n"<<endl;
cout<<" \n"<<endl;
cout<<"6)Divide -> r \n";
x=(r1/r2)*cos(phi1-phi2);
y=(r1/r2)*sin(phi1-phi2);
cout<<"z1= "<<x<<" +j "<<y<<endl;
system("pause");
return 0;
}

